Na aula 16 de hoje, 25 de fevereiro, das 20:10h às 22h, da disciplina de Mecânica Quântica I, os estudantas da disciplina deverão fazer um resumo da palestra do III Encontro de Física-Matemática da UFCG, sobre Supersimetria (SUSY) em Mecânica Quântica gravada no IQUANTA da UFCG, campus sede, na quarta-feira, 23 de fevereiro.
SUSY em Mecânica Quântica
O vídeo dessa palestra foi dividido em 3 partes e estão disponíveis no Youtube, o link dele será colocado aqui. Mostramos a representação das supercargas, geradora da álgebra SUSY, em termos de operadores diferencial de primeira ordem, mutuamente adjuntos, propostos por Witten(1981), para obter o operador hamiltoniano da mecânica quântica não-relativística. O superpotencial é uma função da coordenada de posição, f(x) e, em homenagem a Witten, escrevemos f=W(x).
Parte I Equação de Schrödinger (1926) independtendente do tempo e a interpretação probabilística de Max Born(1927).
Parte II
Parte III
SUSY e o Método de Fatoração em Mecânica quântica, para o oscilador harmônico simples. O operador hamiltoniano H é escrito em termos dos operadores escada de levantamento e abaixamento dos níveis de energia, resultando no operador de número N, adicionado do autovalor de energia do estado fundamental, E(0), ou seja:
H =(1/2m)p2+V(x)=N+E(0)
NΨ(n)=nΨ(n)
Com, n=0, 1 , 2, ...
O potencial do oscilador harmônico simples é dado por uma função do segundo grau, na coordenada de posição:
V(x)=(1/2)mω2x2
Portanto, a equação de Schrödinger independente do tempo fornece os autovalores discretos para os n-nésimos estados excitados:
HΨ(n)=E(n)Ψ(n)
Neste caso do oscilador harmônico, a fatoração do hamiltoniano que aparece no setor bosônico do hamiltoniano SUSY, o termo cinético torna-se um operador com derivada de segunda ordem:
No caso do oscilador harmônico unidimensional supessimétrico(SUSY), colocando um bóson e retirando um férmion e vice-versa, o valor da energia do hamiltoniano SUSY não é alterada.







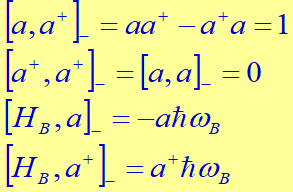







Presente (Maycon)
ResponderExcluirSilvanira, presente
ResponderExcluir