Nesta Aula 04 da disciplina de Instrumentação em Ciência da Natureza e suas Tecnologias I, Professor Rafael, dentro da programação das aulas remotas da UFCG, período 2021.1, nesta terça, 9 de dezembro, será visto o conceito de velocidade instantânea, aquela medida no velocímetro dos automóveis.
Segunda Lista de exercícios propostos: Velocidade Média e Velocidade Instantânea.
Foi visto: Movimento
O estado de Movimento e Repouso depende de um referencial. Se a distância variar em relação ao referencial dizemos que o corpo está em movimento. Se a distância não mudar em relação ao referencial dizemos que o corpo está em repouso. Por exemplo, imagine você dentro de um carro, em movimento, para o observador fora do carro ele verá você em movimento. Se o observador estiver dentro do carro ele verá você em repouso.
Este é um dos assuntos mais antigo da ciência, sendo que é preciso definir matematicamente o que é um referencial em Física?
Um referencial em Física no espaço tridimensional, é um ponto de observação, tendo 3 eixos com orientações positivas e o observador na origem do sistema de coordenadas, com todos os instrumentos de mediada para o fenômeno em estudo. Em um movimento na reta, basta um eixo com orientação positiva (movimento unidimensional).
Velocidade Média
A velocidade Média é a distância total percorrida dividida pelo tempo gasto, seguindo o deslocamento de um corpo, em uma curva ou reta. Ela representa um valor hipotético para a velocidade. Por exemplo, se você viajar de Alagoa Grande-PB para Campina Grande pela BR 230, percorrerá uma distância de 60km com uma velocidade média de 90km/h, chegará em 40 minutos. Note que podemos ter diversas velocidades neste percurso, digamos, menos de 90km/h e acima de 90km/h, mas na média foi 90km/h. Agora, você poderá escrever a equação da velocidade como sendo a distância dividido pelo tempo,
Nos livros- textos, o deslocamento escalar, em geral, é representado pela letra s da palavra em inglês space, mas você poderá usar a letra d de distância.
Unidades de medidas no SI: distância é m(metro), tempo é s(segundo) e velocidade m/s.
👍 Na escola da educação básica, você estudou o conceito de velocidade média, taxa de variação da posição pelo tempo, ou seja, v=Δx/Δt, lê-se delta x por delta t. Com ΔX= variação da posição, sendo a distância total percorrida, igual a posição final menos a posição inicial e Δt=tempo gasto no percurso total.
Exemplo. Considerando o exemplo acima a distância percorrida é 60km e o tempo gasto pelo carro foi 40 minutos. Qual a velocidade média em km/h?
Solução
d=60km e t=40min. Neste caso, devemos antes transformar o minuto para hora. Sabemos que 1h=40min, portanto, 1min=(1/60)h. Resulta que, 40mim=(40/60)h. Ao invés de dividir é melhor simplificar, ou seja, cortando o zero e dividindo o numerador e o denominador por 2, obtemos:
t= 40mim=(40/60)h= (2/3)h. Agora, para calcular a velocidade média, basta dividir e, tendo em mente, que a unidade de velocidade do carro será km/h.
Usando a regra de divisão de fração: (a/b)/(c/d)=(ad)/(bc), isto é, fixamos a fação do numerador e multiplicamos pela inverso da fração do denominador.
v=d/t=(60/40)km/min=(60/1)/(2/3)km/h
Comparando, vemos que: a=60, b=1, c=2 e d=3. Finalmente, obtemos:
v=(60/1)/(2/3)=(60x3)/2=180/2=90, ou seja, v=90km/h.
Observação.
Note que para transformar de km/min para km/h
km/min=[1/(1/60)]km/h=60km/h. Neste caso, para transformar de km/min basta multiplicar por 60. Logo,
v=d/t=(60/40)km/min=[(60x60)/40]km/h=[3600/40]km/h=90km/h.
No caso de transformar 1km/h para m/s, multiplicamos ou dividimos por 3,6?
Lembre-se que 1km=1000m e 1h=60min=60x60s=3600s. Portanto,
1km/h=1000m/3600s=(1 /3,6)m/s, ou seja, 1m/s=3,6km/h.
Note que existe muita maneiras de transformar as unidades de velocidade, seria melhor você trabalhar com as unidades fundamentais e simplificar as frações, pois você só poderá multiplicar por 3,6 para obter a unidade de velocidade em m/s, somente no caso em que a velocidade for dada em km/h.
O procedimento que irá direto sem ter dúvida se multiplica ou divide é fazer o cálculo direto como no exercício 1.
Velocidade Instantânea
A velocidade Instantânea representa o valor real em um dado instante de tempo. Ela fornece o valor absoluto da velocidade em cada instante de tempo, bem próximo um do outro, podendo ser igual a velocidade média. Newton, após estudar a cinemática de Galileu(Morreu em 1642, ano em que nasceu Newton) ao definir a velocidade instantânea, ele introduziu o artifício de limite com a variação do tempo cada vez menor.
Entendendo o significado físico de Velocidade
Na prática, você poderá ver a velocidade instantânea de um carro, olhando para o velocímetro, quando estiver com a velocidade limite permite pela lei de trânsito brasileira, 110km/h, significa que viajando sempre com essa velocidade, o carro percorrerá 110km em uma hora. Isso é o significado físico de velocidade.
Definição do limite(Lim) da velocidade escalar média com a variação do tempo tendendo a zero é de fato a velocidade instantânea, a saber:
Lê-se derivada de s em relação a t, que é representada por
Interpretação geométrica, fazendo s=x, obtemos:
Regra de Derivada de polinômios de segundo grau.
Vamos calcular a velocidade instantânea usando a definição de derivada, para o caso em que s=t2 vamos calcular a seguinte variação: Δs=s(t+Δt)-s(t).
Usando o produto notáveis, (a+b)^2 = a2 + b2 + 2ab, obtemos:
s=t2 ⇒ s(t+Δt)= (t+Δt)2 = t2 + Δt2 +
2t Δt
⇒ Δs/Δt=[s(t+Δt)-s(t)]/Δt=
(t2 + Δt2 + 2tΔt-t2)/Δt
= Δt2 /Δt+ 2t Δt/Δt= Δt+2t.
Portanto, aplicando o limite de Δt tendendo a zero, o termo Δt tende a zero e restando 2t, ou seja, a velocidade instantânea
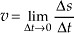torna-se: v=dx/dt=dt2/dt =2t.Generalizando, considerando a coordenada de posição sendo o tempo elevado a n e multiplicada por uma constante, temos:
Exemplo: 
Seja a=1/2 e n=2. 
⇒ v=(2/2)t=t.
Seja a=1/2 e n=2. ⇒ v=(2/2)t=t.Seja a=1/2 e n=3 ⇒ v=(3/2)t2 .
Função horária como sendo um polinômio de terceiro grau.
Exemplo. 1) Considere um automóvel se deslocando de acordo com a seguinte função horária, tendo seus valores de tempo e de distância percorrida medidos no sistema internacional de medida(SI), dada por:
s(t) = 2t3 + 4t2 - 5t + 7 (SI)
Qual a velocidade do móvel no instante após 10 segundos?
Solução
Calculando a derivada de um polinômio de terceiro grau, aplicando a propriedade da soma das derivadas e a regra de potência, obtemos um polinômio de segundo grau, ou seja,
Agora, para obter a v(10s), basta substituirmos o tempo por 10, sem os segundos, pois aqui todas as grandezas estão no SI. Portanto, obtemos a velocidade em m/s:
v(10s)=(6x100+8x10-5)m/s=(600+80-5)m/s=675m/s
Ou poderíamos ter calculado v(10), e no resultado final colocar m/s. Pois, como estamos usando o SI, a unidade de velocidade é m/s.
Portanto, v(10s)=675m/s.
UFCG-CES-UAFM
Professor Rafael Rodrigues
Lista de Exercícios 2
1) Considere a seguinte função horária de uma moto em movimento, tendo seus valores de tempo e de distância percorrida medidos no sistema internacional de medida(SI), dada por:
s(t) = 5t3 + 0,5t2 - 2t + 1 (SI)
Determine a velocidade instantânea.
a) Usando o conceito de limite, qual a velocidade do móvel no instante após 8 segundos?.
b) Usando a regra de derivação, determine v(8).
2) a) Dizer quais são as principais contribuições de Galileu para a cinemática. b) Como era a pesquisa em Física antes de Galileu?
3) Considere um carro se movendo em linha reta com aceleração constante 6m/s² e velocidade inicial 40 km/h. Qual a função horária do deslocamento ΔX?.
ΔX= variação da posição, sendo a distância total percorrida, igual a posição final menos a posição inicial.
Lembre-se: ΔX=
4) Qual o tempo que um carro em movimento leva até parar, tendo partido com uma velocidade inicial de 60Km/h e tenha sofrido uma desaceleração de 4m/s²?
5) Enem de 2012 (Questão 66, Caderno amarelo, prova de Ciências da Natureza e suas Tecnologias).
Uma empresa de transportes precisa efetuar a entrega de uma encomenda o mais breve possível. Para tanto, a equipe de logística analisa o trajeto desde a empresa até o local da entrega. Ela verifica que o trajeto apresenta dois trechos de distâncias diferentes e velocidades máximas permitidas diferentes. No primeiro trecho, a velocidade máxima permitida é de 80 km/h e a distância a ser percorrida é de 80 km. No segundo trecho, cujo comprimento vale 60 km, a velocidade máxima permitida é 120 km/h.
Supondo que as condições de trânsito sejam favoráveis para que o veículo da empresa ande continuamente na velocidade máxima permitida, qual será o tempo necessário, em horas, para a realização da entrega?
6) ENEM 2021. Nas estradas brasileiras existem vários aparelhos com a finalidade de medir a velocidade dos veículos. Em uma rodovia, cuja velocidade máxima permitida é de 80 km h−1, um carro percorre a distância de 50 cm entre os dois sensores no tempo de 20 ms. De acordo com a Resolução n. 396, do Conselho Nacional de Trânsito, para vias com velocidade de até 100 km h−1, a velocidade medida pelo aparelho tem a tolerância de +7 km h−1 além da velocidade máxima permitida na via. Considere que a velocidade final registrada do carro é o valor medido descontado o valor da tolerância do aparelho.
Nesse caso, qual foi a velocidade final registrada pelo aparelho?
7) ENEM 2021. Os acidentes de trânsito são causados geralmente por excesso de velocidade. Em zonas urbanas no Brasil, o limite de velocidade normalmente adotado é de 60 km h−1. Uma alternativa para diminuir o número de acidentes seria reduzir esse limite de velocidade. Considere uma pista seca em bom estado, onde um carro é capaz de frear com uma desaceleração constante de 5 m s−2 e que o limite de velocidade reduza de 60 km h−1 para 50 km h−1.
Nessas condições, a distância necessária para a frenagem desde a velocidade limite até a parada completa do veículo será reduzida em um valor mais próximo de8) ENEM 2018. Um piloto testa um carro em uma reta longa de um autódromo. A posição do carro nessa reta, em função do tempo, está representada no gráfico.
Quais são os pontos em que a velocidade do carro é menor e maior?
9) ENEM 2013. Conta-se que um curioso incidente aconteceu durante a Primeira Guerra Mundial. Quando voava a uma altitude de dois mil metros, um piloto francês viu o que acreditava ser uma mosca parada perto de sua face. Apanhando-a rapidamente, ficou surpreso ao verificar que se tratava de um projétil alemão.
PERELMAN, J. Aprenda física brincando. São Paulo: Hemus, 1970.
O piloto consegue apanhar o projétil, pois
a) ele foi disparado em direção ao avião francês, freado pelo ar e parou justamente na frente do piloto.
b) o avião se movia no mesmo sentido que o dele, com velocidade visivelmente superior.
c) ele foi disparado para cima com velocidade constante, no instante em que o avião francês passou.
d) o avião se movia no sentido oposto ao dele, com velocidade de mesmo valor.
e) o avião se movia no mesmo sentido que o dele, com velocidade de mesmo valor.
10) ENEM 2013. Antes das lombadas eletrônicas, eram pintadas faixas nas ruas para controle da velocidade dos automóveis. A velocidade era estimada com o uso de binóculos e cronômetros. O policial utilizava a relação entre a distância percorrida e o tempo gasto, para determinar a velocidade de um veículo. Cronometrava-se o tempo que um veículo levava para percorrer a distância entre duas faixas fixas, cuja distância era conhecida. A lombada eletrônica é um sistema muito preciso, porque a tecnologia elimina erros do operador. A distância entre os sensores é de 2 metros, e o tempo é medido por um circuito eletrônico.
Qual o tempo mínimo, em segundos, que o motorista deve gastar para passar pela lombada eletrônica, cujo limite é de 40 km/h, sem receber uma multa?
Blog rafaelrag
aluno genezio
ResponderExcluirpresente
Presente! Geraldo Jr
ResponderExcluirPresente
ResponderExcluir