Foi visto.
Esperança matemática e a variância para as variáveis aleatórias discretas.
Veja o vídeo.
Desvio padrão e a densidade de probabilidade.
A altura, o tempo, medida da temperatura, energia, coordenada de posição, velocidade e a verificação da pressão são exemplos de variáveis aleatórias continuas. Uma densidade de probabilidade f(x), satisfaz a duas condições.
(i) A função contínua f(x) é maior ou igual a zero, ou seja,
0≤ f(x)
(ii) a integral de f(x) de menos o infinito a mais o infinito é um
(∫-∞^+∞f(x)dx=1.)
F (x) = P (X ≤ x),
0 ≤ F (x) ≤ x1.
Veja o vídeo.
Distribuição de probabilidade para uma variáveis aleatórias discreta e contínua com o professor Rafael.
Portanto, com c=-3/2=-1,5, a densidade de probabilidade f(x)=2x-3/2.
Qual a probabilidade, com a variável aleatória X, assumindo valores no intervalo, 0<X<1,5?
Solução.
Queremos saber, P(0<X<1,5)=?
Nesta caso iremos calcular a seguinte integral definida:
P(0<X<1,5)=∫1,50(2x-3/2)dx=2∫1,50xdx-(3/2)∫1,50dx= (1,5)2-(1,5)2=0.
⇔P(0<X<1,5)=0.
Note que a primeira condição para f(x) ser uma densidade de probabilidade é
f(x)>0, ou seja, para que a probabilidade P seja 0<P<1, temos:
2x-1,5>0, isto é, x>3/4=0,75.
Logo, x>0,75.
Note que não podemos calcular a probabilidade P(0<X<0,5), pois neste caso, a densidade de probabilidade seria negativa,
f(x=0,5)=2.0,5-1,5=1-1,5=-0,5<0.
Distribuição Normal.
https://youtu.be/_TwduG70UiY?si=t9bB-OK2cukYhYfK
Tabela Z.
Em uma densidade de probabilidade gaussiana a esperança matemática(média) é E[X]= 𝞵 e V[x]=𝞼² é a variância de X.
Interpretação geométrica da integral definida, ela representa a área abaixo da curva. Portanto, a probabilidade de uma variável aleatória, em um certo intervalo, é a área abaixo da curva da densidade de probabilidade.
Exercícios sobre a Distribuição Normal padrão(ou reduzida).
A densidade de probabilidade de uma distribuição Normal padrão, f(z), é representado por N(0,1). Agora, a esperança matemática(média) é E[Z]= 0 e V[Z]=1 é a variância de Z.
Considere que a variável aleatória Z seja a temperatura de um termômetro associada a Distribuição Normal padrão N(0,1). Qual a probabilidade de escolher um termômetro que acuse a leitura da temperatura entre 1, 42 e 2,64 graus Celcius?
Solução
É preciso calcular a probabilidade
P(1,42≤ Z ≤ 2,64)=?
Desenhe o gráfico da gaussiana, para visualizar melhor.
Tabela Z: A tabela Z fornece os valores de f(z) para diferentes valores de z. Para encontrar P(Z < 1,42), procure o valor de 2 na coluna "z" e o valor na coluna 4 e descendo você encontrará o valor correspondente na coluna "Área". O valor encontrado será a probabilidade desejada.
A distribuição normal, também conhecida como distribuição gaussiana, é uma das distribuições de probabilidade mais importantes em estatística e tem diversas aplicações em diferentes áreas do conhecimento.
A Estatística é a base para diversos testes estatísticos, como o teste t e o teste z.
Ela pode ser utilizada para modelar erros em modelos estatísticos, como a regressão linear.
Permite calcular probabilidades de ocorrência de eventos em diversos fenômenos.
Ciências Naturais: É utilizada para descrever a distribuição de diversas variáveis, como temperatura, altura, peso, pressão sanguínea e resultados de testes de inteligência.
É aplicada em estudos de fenômenos físicos, como a distribuição de erros de medição.
Finanças:
É utilizada para modelar o comportamento de preços de ativos financeiros. É aplicada em cálculos de risco e retorno de investimentos.
Engenharia:
É utilizada no controle de qualidade de processos industriais. É aplicada na análise de confiabilidade de sistemas.
Ciência da Computação:
É utilizada em algoritmos de aprendizado de máquina e inteligência artificial. É aplicada na análise de dados e reconhecimento de padrões.
Características da Distribuição Normal:
É uma distribuição contínua e simétrica em forma de sino.
A média, a mediana e a moda têm o mesmo valor.
A área sob a curva representa a probabilidade total, que é igual a 1.
A distribuição normal padrão f(Z) tem média 0 e desvio padrão 1.
Importância da Distribuição Normal.
O Teorema Central do Limite garante que a distribuição da média de uma amostra tende a uma distribuição normal à medida que o tamanho da amostra aumenta.
A distribuição normal permite fazer previsões e inferências estatísticas com base em dados amostrais.
A distribuição normal padrão permite comparar dados de diferentes distribuições. Claro, vamos calcular as probabilidades para a distribuição normal N(60; 25).
a) Probabilidade com a vaiável aleatória X entre 50 e 70: o cálculo é feito com a distribuição normal padrão
Z=(X-𝞵 )/𝞼.
1. Calcule os valores de Z:
X=50 ⇔Z1= (50 - 60) / 5 = -2
X=60 ⇔ Z2 = (70 - 60) / 5 = 2
2. Encontre as probabilidades correspondentes: use a tabela Z.
P(Z < -2) = 0,0228
P(Z < 2) = 0,9772
3. Calcule a probabilidade desejada: fazendo cálculo da diferença.
P(50 < X < 70) = P(-2 < Z < 2) = P(Z < 2) - P(Z < -2) = 0,9772 - 0,0228 = 0,9544
b) Probabilidade superior a 55:
1. Calcule o valor de Z:
Z = (55 - 60) / 5 = -1
2. Encontre a probabilidade correspondente:
P(X > 55) = P(Z > -1) = 1 - P(Z < -1) = 1 - 0,1587 = 0,8413
Resultados:
a) A probabilidade de X estar entre 50 e 70 é de 0,9544 ou 95,44%.
b) A probabilidade de X ser superior a 55 é de 0,8413 ou 84,13%. A probabilidade P(Z < 2) representa a área sob a curva da distribuição normal padrão à esquerda do valor z = 2. Para calcular essa probabilidade, utilizamos a função de distribuição cumulativa da distribuição normal padrão, denotada por f(z).
A função f(z) não possui uma fórmula analítica simples, mas pode ser calculada numericamente ou encontrada em tabelas estatísticas.
Métodos para calcular P(Z < 2):
Tabela Z: A tabela Z fornece os valores de f(z) para diferentes valores de z. Para encontrar P(Z < 2), procure o valor de 2 na coluna "z" e o valor correspondente na coluna "Área". O valor encontrado será a probabilidade desejada.
Calculadora estatística: A maioria das calculadoras científicas possui funções estatísticas que permitem calcular f(z). Procure a função "normalcdf" ou similar e insira os valores de z desejados.
Software estatístico: Softwares como R, Python (com a biblioteca SciPy) ou Excel possuem funções para calcular f(z).
Exemplo:
Usando uma tabela Z ou calculadora, encontramos que P(Z < 2) ≈ 0,9772.
Interpretação:
A probabilidade P(Z < 2) ≈ 0,9772 significa que há aproximadamente 97,72% de chance de uma variável aleatória com distribuição normal padrão assumir um valor menor que 2.
Função de distribuição acumulada
F (x) = P (X ≤ x)
Teorema central do limite
Segundo o Teorema Central do Limite, para grandes amostras, independentemente da distribuição da variável de interesse, a distribuição das médias amostrais serão aproximadamente normalmente distribuídas, e tendem a uma distribuição normal à medida que o tamanho de amostra cresce.
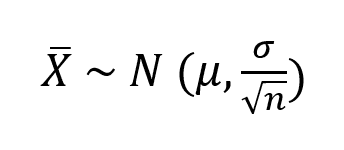
Sendo,
μ = média das medidas individuais X
σ = desvio padrão das medidas individuais X
n = tamanho amostral
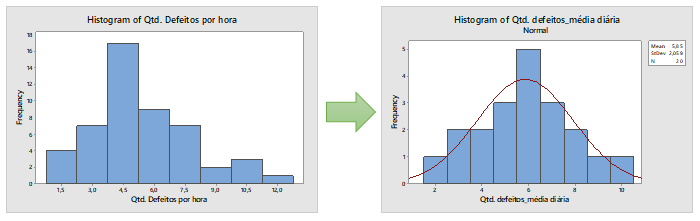
No exemplo abaixo, uma empresa mede a quantidade de defeitos em um lote de 100 produtos a cada duas horas. O histograma dos dados coletados a cada duas horas representa uma distribuição diferente da normal.
Em um segundo momento, os dados foram agrupados diariamente, ou seja, foi calculado a média de defeitos do dia de produção e utilizou-se o valor da média diária para gerar um novo histograma. Desta vez a distribuição já é normal.
Perguntas de probabilidade
As perguntas sobre a probabilidade de distribuição normal padrão podem parecer complexas, mas a chave para resolvê-las é compreender o que a área sob a curva representa.
A área total sob uma curva de distribuição normal padrão é de 100% (ou seja, "1" como um decimal). Por exemplo, a metade esquerda da curva é 50% ou 0,5. Portanto, a probabilidade de uma variável aleatória aparecer na metade esquerda da curva é 0,5.
É claro que nem todos os problemas são simples assim, e é por isso que há uma tabela-z. Tudo o que uma tabela-z faz é medir essas probabilidades (ou seja, 50%) e colocá-las em desvios-padrão da média. A média está no centro da distribuição normal padrão e uma probabilidade de 50% é igual a zero desvios padrão.
Como interpretar a curva da Distribuição Normal?
Conseguimos desenhar uma curva de distribuição normal tendo apenas dois parâmetros: média e desvio padrão.
Considerando a probabilidade de ocorrência de um fenômeno, a área sob a curva representa 100%. Isso quer dizer que a probabilidade de uma observação assumir um valor entre dois pontos quaisquer é igual à área compreendida entre esses dois pontos.
O ponto mais alto na curva, representa o valor com a maior moda do processo, ou seja,, o valor que mais aparece na base de dados. Esse é representado na curva pelo corte central deste diagrama.
Os outros cortes verticais, representam o desvio padrão em relação a média, ou seja, temos uma faixa de valores que significa a soma ou subtração de um desvio padrão em relação a média.
Outro detalhe importante e conhecido da curva de distribuição normal é que cada faixa de valores representa uma certa probabilidade de ocorrência.
Neste exemplo, na primeira faixa, de menos 1 desvio padrão até 1 desvio padrão, está compreendido 68,26% da base de dados. Se ampliarmos um pouco mais e pegarmos a faixa que vai de mais até menos 2 sigma, já teremos 95,44% de possibilidade de ocorrência.
Por fim, se pegarmos a faixa mais ampla dessa distribuição, ou seja, mais ou menos 3 sigma. Essa faixa já representa 99,74% dos dados.
Essa região, chamamos de faixa natural de variação do processo. A estatística entende que um processo possui uma certa variabilidade, ou seja, trabalha dentro de uma faixa de valores, com determinada variação.
Se esse processo é um processo estável, significa que a variação desse processo vai acontecer dentro dessa faixa de valores.
Se tiver algum problema ou perturbação maior no processo, pode ser que ele produza um resultado que não é o esperado, ou que não era provável, um resultado muito acima ou muito abaixo do normal.
Esse resultado seria um ponto fora dessa faixa de variação natural do processo, ou seja, o famoso ponto fora da curva. Um ponto cuja probabilidade é tão baixa de acontecer que o denominamos de outlier.
Com esse conceito de distribuição normal contextualizado para uma empresa ou processo, é possível comparar e entender, que quando se tem uma base de dados representada pela curva de Gauss compreendida entre uma faixa de mais ou menos 3 sigma, esse processo é considerado estável.
Como montar uma curva de Distribuição Normal?
Para melhor explicar como montar uma curva de distribuição normal, que tal acompanhar um simples exemplo junto comigo? Imagine que em uma sala de aula, o professor anotou a idade de cada um de seus quarenta alunos presentes.
Após coletar os dados ele percebeu que a distribuição da idade dos alunos possuía o formato de uma distribuição normal com média e desvio padrão respectivamente de, μ= 23 e σ= 2.
O objetivo então, é projetar a curva de distribuição normal correspondente aos valores de média e desvio padrão da idade dos alunos. Além de determinar qual é o percentual de alunos com idade entre 21 e 25 anos. E também qual o percentual de alunos com idade entre 19 e 27 anos.
De antemão, já sabemos que o valor de média igual a 23 anos, estará no centro da nossa distribuição. Que ao mesmo tempo é o ponto de valor mais alto da curva.
Como a distribuição normal começa próximo do menos 3 sigma e termina próximo do mais 3 sigma, sabemos que a curva irá começar próximo ao valor de 23-3*2, ou seja 17 anos, e vai ter o decaimento próximo de 23+3*2, ou seja, 29 anos.
Com tais conceitos aplicados já é possível um esboço, veja!
Os alunos com idade entre 21 e 25 anos, representam exatamente ± 1σ, ou seja, 68,26% dos alunos, já os alunos que possuem idade entre 19 e 27 anos, representam a variação de ± 2σ, representando assim 95,44% do total de alunos. Isso representa aproximadamente 38 alunos.
Aplicações Práticas do Modelo de Distribuição Normal Padrão
A distribuição normal padrão pode ajudá-lo a descobrir quais disciplinas você está obtendo boas notas e quais você deve estudar mais, de acordo com as notas que vêm obtendo.
Então, você pode pensar: se fui melhor nessa matéria do que em outra, com certeza sou melhor nessa! Mas você pode estar enganado!
Você só pode dizer que é melhor em um assunto específico se obtiver uma pontuação com um certo número de desvios padrão acima da média. O desvio padrão informa a intensidadecom que seus dados são agrupados em torno da média. Ele permite que você compare diferentes distribuições que possuem diferentes tipos de dados - incluindo diferentes meios.
Por exemplo, se você obtiver uma pontuação de 90 em matemática e 95 em português, poderá pensar que é melhor em português do que em matemática. No entanto, em matemática, sua pontuação é de 2 desvios padrão acima da média. Em português, é apenas um desvio padrão acima da média.
Isso significa que, em matemática, sua pontuação é muito maior do que a maioria dos alunos (sua pontuação se apresenta na cauda da distribuição normal).
Com base nesses dados, você realmente teve um desempenho melhor em matemática do que em português!
Quando utilizar a Distribuição binomial?
Ao iniciar um projeto Seis Sigma, o Green ou Black Beltdeve verificar qual é o tipo de dado (contínuo ou discreto) que está lidando na saída do processo. Isto vai determinar quais as ferramentas que serão utilizadas no desenvolvimento do projeto.
Cabe a este profissional definir qual das inúmeras distribuições estatísticas é a que melhor representa o processo que está sendo estudado. As distribuições estatísticas podem ser divididas em dois grandes grupos:
- Distribuição Discreta (Atributos)
- Distribuição Contínua (Variável).
As distribuições discretas por sua vez, devem ser utilizadas para modelar situações em que a saída de interesse só pode assumir valores inteiros (discretos) como, número de caras ou coroas, 0 ou 1 para falha ou sucesso, ou 0,1,2,3,... como o número de ocorrências de um determinado evento de interesse por exemplo.
Tipos de Distribuição estatística discreta
1. Distribuição de Poisson
A distribuição de Poissoné uma distribuição discreta de probabilidade aplicável a ocorrências de um número de eventos em um intervalo específico. Para reconhecer uma distribuição de Poisson, basta observar os 3 aspectos a seguir:
- O experimento calcula quantas vezes que um evento ocorre em um determinado intervalo de tempo, área, volume, etc
- A probabilidade do evento ocorrer é a mesma para cada intervalo
- O número de ocorrências de um intervalo é independente do outro.
Alguns exemplos de distribuição de Poisson são:
- Usuários de computador ligados à Internet
- Clientes chegando ao caixa de um supermercado
- Acidentes com automóveis em uma determinada estrada
- Erros de digitação por um certo período de tempo
- Número de carros que chegam a um posto de gasolina
- Número de falhas em componentes por unidade de tempo
- Número de requisições para um servidor em um intervalo de tempo.
2. Distribuição Binomial
Teoricamente, a distribuição binomial é a distribuição de probabilidade e estatística discreta do número de sucessos decorrentes de uma determinada sequência de tentativas, que seguem à seguintes características:
- Espaço amostral finito
- Apenas dois resultados possíveis (sucesso ou fracasso) para cada tentativa
- Todos os elementos devem possuir possibilidades iguais de ocorrência
- Eventos devem ser independentes uns dos outros.
A Distribuição Normal é uma distribuição de probabilidade contínua e simétrica que representa o comportamento de um fenômeno natural de forma aleatória.
No século XVIII, alguns matemáticos e físicos desenvolveram uma função de probabilidade que conseguia obter os erros experimentais em medidas físicas. No entanto, diversos fatores estavam entre suas causas e, em alguns casos, os motivos não eram identificáveis.
Somente em meados do século XIX, Friedrich Gauss, com seus estudos sobre eventos da natureza, observou um comportamento padrão entre as amostras estudadas por ele.
Esse comportamento, posteriormente, foi apresentado como aCurva de Gauss. Que mostrava que grande parte dos eventos ficam em torno de um valor médio, com uma certa variabilidade.
Então, surgiu a Distribuição Gaussiana ou Normal. Ela é o principal modelo probabilístico contínuo, sendo muito utilizada pelas áreas de Estatística, Probabilidade e Estocástica.
Continue lendo esse artigo e descubra quais são as dúvidas mais frequentes na Distribuição Normal, hoje você irá aprender:
- O que é Distribuição Normal?
- Qual a utilidade da Distribuição Normal?
- O que é Escore Z derivado da curva normal?
- Como determinar se a Distribuição é Normal?
- Teorema central do limite
- Perguntas de probabilidade
- Como interpretar a curva da Distribuição Normal?
- Como montar uma curva de Distribuição Normal?
- Aplicações Práticas do Modelo de Distribuição Normal Padrão
- Tipos de Distribuição estatística discreta
Vamos lá?
O que é Distribuição Normal?
A distribuição normal, também conhecida como distribuição gaussiana, é uma curva simétrica em torno do seu ponto médio, apresentando assim seu famoso formato de sino.
Uma distribuição estatística é uma função que define uma curva, e a área sob essa curva determina a probabilidade de ocorrer o evento por ela correlacionado.
E o que é distribuição normal? Me arrisco dizer, que é a mais importante dentre as distribuições estatísticas.
A curva de distribuição normal representa o comportamento de diversos processos nas empresas e muitos fenômenos comuns, como por exemplo, altura ou peso de uma população, a pressão sanguínea de um grupo de pessoas, o tempo que estudantes gastam em uma prova.
A distribuição normal pode ser usada para aproximar distribuições discretas de probabilidade, como a distribuição binomial. Além disso, a distribuição normal serve também como base para a inferência estatística clássica.
Nela, a média, mediana e modados dados possuem o mesmo valor.
Qual a utilidade da Distribuição Normal?
A Distribuição Normal é essencial para calcular diferentes situações, seja para estudo da ocorrência de fenômenos físicos, pesquisas dentro de uma empresa ou para análises financeiras.
Além disso, através dessa distribuição é possível fazer cálculos com um grande número de dados, pois é utilizada uma média e existe o desvio-padrão. Com essas proporções pré-definidas, os cálculos conseguem resumir os valores de maneira mais prática.
O que é Escore Z derivado da curva normal?
O escore Z é uma unidade de desvio-padrão que mede o quanto um elemento está distante da média da população, ou seja, dos escores amostrais. Para se aprofundar mais no assunto, assista o vídeo a seguir:
Como determinar se a Distribuição é ormal?
Para determinar se uma determinada variável aleatória segue uma distribuição normal, basta verificar se essa segue a função densidade de probabilidade, dada por:
Onde a média e ² é a variância de x.
A notação é usada para denotar tal distribuição.
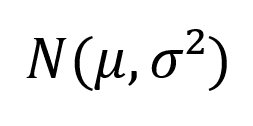
Para calcularmos então a probabilidade de um resultado, basta integrar a função f(x) em relação a x, com os limites de integração representando a faixa de valores que se quer obter a probabilidade.
Vale notar que a integral da função densidade de probabilidade normal, não possui solução analítica, sendo assim, seu cálculo deve ser realizado através de um método numérico.
Para sanar tal dificuldade a função pode ser padronizada com a substituição dos parâmetros por μ=0 e σ²=1. Essa abordagem é dada pela definição de uma nova variável aleatória Z, chamada de variável aleatória normal padronizada.
Se x for uma variável aleatória normal com média E(x)=μ e variância V(x)=σ², a variável aleatória Z=(x−μ)/σ será uma variável aleatória normal, com E(Z)=0 e V(Z)=1. Ou seja, Z é uma variável aleatória normal padrão.
Dessa forma, é possível obter a área sob a curva da normal padrão de forma analítica, e então obter a área entre dois pontos sob a curva, diretamente com o uso de uma tabela de conversão, e essa área representa uma probabilidade.
Blog rafaelrag





















Ok
ResponderExcluirOk
ResponderExcluirOk
ResponderExcluirOk
ResponderExcluirok
ResponderExcluirOk!
ResponderExcluirOk
ResponderExcluirOk
ResponderExcluirOk
ResponderExcluir